Die natürlichen Halbtonschritte
Die Stammtöne, die auf der vorigen Seite vorgestellt wurden, haben eine Eigenschaft, die man ihnen nicht ansieht: sie sind nicht gleich weit von einander entfernt. Zwischen zwei Noten liegt entweder ein Ganztonschritt oder ein Halbtonschritt. Zwei Halbtonschritte sind zusammen so groß wie ein Ganztonschritt.
Ich nenne die "natürlichen Halbtonschritte" so, weil man für sie keine Vorzeichen
braucht, sie liegen einfach zwischen Stammtönen.
Dass es Ganz- und Halbtonschritte gibt ist
nicht logisch, aber sie existieren nun mal aufgrund der Physik, die hinter den Tönen steht. Ihre
Auswirkungen sind musikalisch: die beiden klingen verschieden und haben Auswirkungen auf das,
was Töne ausdrücken.
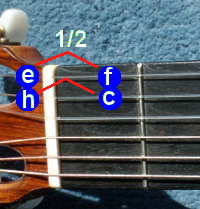
Die natürlichen Halbtonschritte liegen zwischen den Tönen e - f und h - c.
Die sieben Stammtöne (der achte heißt so wie der erste), die unsere Musikkultur benutzt,
heißen
c - d - e - f - g - a -
h - c.
Hier sind die Halbtonschritte in der Reihe von c bis
c unterstrichen. Alle anderen Töne sind einen Ganztonschritt oder zwei
Halbtonschritte von einander entfernt.
Inhaltliche Auswirkungen
Die Tatsache, dass die Abstände zwischen Tönen nicht gleichmäßig sind, sondern ungerecht
verteilt, macht die Musik! Hier liegt die Ursache für verschiedene Tonleitern, für
unterschiedlich klingende Akkorde, für Spannung und Entspannung - die meiste Musik ist so, wie
sie ist, weil es diese komischen Halbtonschritte gibt.
Man muss sie sich also merken.
Gitarristen merken sich: die natürlichen Halbtonschritte finden sich auf den beiden höchsten Saiten zwischen der leeren Saite und dem ersten Bund! Bei einem Halbtonschritt liegen die Töne auf einer Saite immer auf direkt benachbarten Bünden, bei einem Ganztonschritt bleibt ein Bund dazwischen frei.
Wer eine Klaviertastatur kennt weiß, dass zwischen den genannten Tönen die schwarzen Tasten fehlen: dort sind die Halbtonschritte. Auch wenn man auf Blockflöten und Posaunen die Halbtonschritte nicht sehen kann: Man hört sie trotzdem!

Woher die Halbtonschritte kommen versuche ich im nächsten Abschnitt zu erklären, welche Rolle sie in der Durtonleiter spielen steht hier.
Der Tonvorrat
Woher kommen eigentlich die Stammtöne mit den Halbtonschritten an bestimmten Stellen?
Überall in der Musiktheorie wird die Stammtonreihe c - d - e - f - g - a - h - c vorausgesetzt. Man kann die Töne mit ♯ und ♭ erhöhen und erniedrigen und einfach alles vom Wohltemperierten Klavier bis zum Freejazz mit ihnen machen - aber woher kommt eigentlich dieser Tonvorrat?
Dass unsere Stammtöne c - d - e - f - g - a - h heißen ist natürlich eine Übereinkunft. In Frankreich sagt man do, re, mi, fa, sol, la, si, auf englisch C, D, E, F, G, A, B.
Dann gibt es kulturelle Grundvoraussetzungen: Welches Tonmaterial eine Musikkultur benutzt ist
Geschmackssache - in Indien oder Indonesien gibt es Tonleitern, die uns hier
sehr fremd vorkommen.
Schon die alten Griechen haben unsere Stammtöne gekannt und ein
gewisser Pythagoras (a²+b²=c² - genau der!) hat mit Obertönen experimentiert, und über die
Obertonreihe
kann man den Tonvorrat auch herleiten.
Die Stammtöne mit der Obertonreihe in drei Schritten finden
1. Man braucht etwas anderes als den Grundton

Grundton und Oktave; Grundton und Oktavquinte.
Man hört so gut wie nie nur einen Ton, wenn man einen Ton hört, sondern mit ihm immer eine Reihe von Obertönen, die für die Klangfarbe verantwortlich sind. In einem Ton sind also immer andere Töne enthalten, die Partialtöne oder Obertöne heißen.
Der erste Partial- oder Teilton eines Tones ist der Grundton selbst, das ist der, den man meint, wenn man "ich höre ein C" sagt. Der zweite Teilton ist seine eigene Oktave, also quasi derselbe Ton. Wenn du eine Saite in der Mitte berührst (nicht herunter drücken - nur sanft berühren) und anschlägst und so den zweiten Partialton erzeugst, hast du also noch keinen wirklich neuen Ton.
2. Der erste andere Ton, der nächste Verwandte
Der dritte Partialton aber ist der erste Verwandte, der nicht dem Grundton selbst entspricht: die Oktavquinte.
Man kann sie hörbar machen, indem man eine Saite im Drittellungspunkt (beim siebten oder 19. Bund) sanft berührt und eher fest anschlägt.

Die gestrichelte Linie soll andeuten: ich lege den Ton tiefer, damit es nicht schnell extrem hoch wird.
Man erzeugt also über dem ersten Ton dessen Oktavquinte. Über dem c ist
das das g.
Diesen neu gefundenen Ton nimmt man als nächsten
Ausgangspunkt und spielt über ihm seine Oktavquinte und fährt dann entsprechend fort.
So bekommt man schnell sehr hohe Töne - deshalb legt man immer "den Neuen" eine oder zwei
Oktaven tiefer. Dadurch erhält man über den nächst möglichen Verwandten jedes Tones die
Stammtöne der Reihe nach.
Am Ende der Prozedur legt man sie alle in eine Oktave und ordnet
sie der Tonhöhe nach, damit das Ergebnis wie eine Tonleiter aussieht.
Achtung: wenn man bei c beginnt, erhält man als siebte Quinte das fis, also fängt man besser bei f an, und erhält so unsere Stammtöne, also die Töne ohne Vorzeichen: f-c-g-d-a-e-h.
3. Reihe der Oktavquinten
Über dem f findet man als dritten Partialton das c, über dem c findet man auf die gleiche Art ein g, darüber das d, darüber das a, dann folgt das e und schließlich das h. Schiebt man die gefundenen Töne in einen Oktavstreifen, erhält man die Stammtonreihe.

Am Ende habe ich auch das fis noch angefügt, um anzudeuten: nach den Stammtönen geht es noch weiter!
Alle zwölf Halbtonschritte
Natürlich kann man auch alle zwölf Halbtonschritte unseres Notensystems durch diese Abfolge von Quinten hervorbringen. In der Grafik unten habe ich beim tiefsten c der Klaviatur angefangen und habe die Oktavquinten direkt in Quinten umgewandelt. Nach dem fis folgen die anderen hochalterierten Töne, denen ich jeweils als kleine Note die enharmonische Verwechslung beigesellt habe. Die letzten Töne sind eis'''' und his'''', die man auf der Klaviatur auch als f'''' und c''''' bezeichnen kann, allerdings finde ich wichtig, sie zunächst mit ihrem "richtigen" Namen anzureden, denn vom ais''' zum f'''' ist es keine Quinte, sondern eine verminderte Sexte, aber das ist eine andere Geschichte...
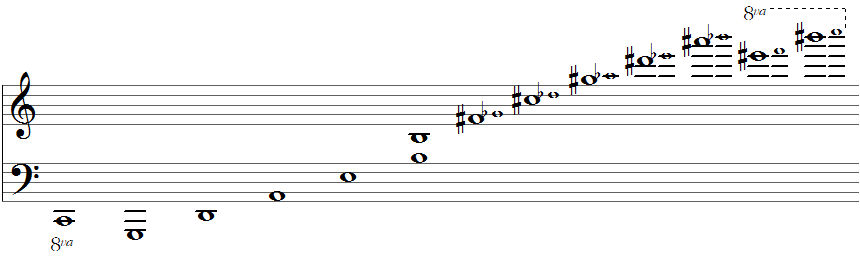
Schwingungen pro Sekunde oder Hertz
Die Halbtonschritte zwischen e - f und h - c ergeben sich einfach aus den physikalischen Tatsachen. Jeder Ton, der über die Quintenabfolge erreicht wurde, hat ja eine bestimmte Tonhöhe oder Frequenz, die in Schwingungen pro Sekunde oder Hertz angegeben wird, und die Halbtonschritte liegen eben dichter bei einander, während bei den Ganztonschritten immer noch ein weiterer (durch Kreuz oder ♭ herzustellender) Halbton dazwischen passt. Die Tonhöhen der eingestrichenen Oktave mit der Schwingungszahl Hertz sehen so aus:

Man sieht recht schnell, dass die Abstände in Hertz zwischen den Tönen unterschiedlich groß
sind: zwischen
c' und d' liegen 32 Hertz, zwischen
d' und e' schon 36. Das ist logisch: Da sich
die Frequenz mit jeder Oktave verdoppelt, gibt es von einer Oktave zur nächsten doppelt so
viel "Platz". Von c' nach c'' sind es 261,6
Hz, von c'' zum c''' 523,3.
Aber die
Töne e' und f' sind nur 19,6 Schwingungen pro
Sekunde von einander entfernt, etwa halb so viel wie der vorhergehende Ganzton, und der
folgende wird dann mehr als doppelt so groß sein, nämlich 42,7 Hertz.
Die
Halbtonschritte in der Stammtonreihe sind also schlicht eine physikalische Tatsache.
Hier eine Darstellung der Stammtonreihe von C aus über zwei Oktaven mit den natürlichen Halbtonschritten:

An anderer Stelle gibt es einen Versuch, die Stammtöne grafisch mit Hilfe von Zollstock, Klaviatur und Gitarrengriffbrett darzustellen.
Die Obertonreihe oder Partialtonreihe
Die Oberton- oder Partialtonreihe ist also quasi eine Grundlage der musikalischen Akustik.
Was es mit ihr auf sich hat? Wenn man einen Ton hört, hört man so gut wie nie nur einen Ton. Jedes Instrument, jeder Klangkörper erzeugt außer dem Grundton, den wir vor allem wahrnehmen weitere Frequenzen, die auch hörbar sind, wenn man sich sehr konzentriert und die Bedingungen gut sind. Welche Obertöne bei einem Instrument besonders hervortreten ist entscheidend für dessen Klangfarbe. Auf Grund der produzierten Obertöne klingt eine Oboe eben wie eine Oboe und nicht wie eine Klarinette.
Klangfarbe
Die Menge der wahrzunehmenden Obertöne und ihre Stärke entscheidet darüber, ob man eine Klangfarbe eher als warm oder als kühler empfindet. Die Gitarre hat einen deutlich wärmeren Ton als ein Klavier (wenn die Saiten nicht total abgespielt sind und nach Gummiband auf Zigarrenkiste klingen), und ein Cembalo, obwohl ein Tasteninstrument, ist klanglich doch nahe bei Gitarre oder Westerngitarre einzuordnen. Wenn man mal eine (elektronisch erzeugte) reine Sinusschwingung hört, die eben keine Obertöne hat, hat man das Gefühl von Kälte und Hohlheit. Eine Querflöte erzeugt deutlich andere (weniger) Obertöne als andere Holzblasinstrumente, und hat deshalb nicht den reichen Ton eines Saxophons.
Obertöne in der Sprache
Auch unsere Sprache funktioniert nur dank der Obertöne - wenn es sie nicht gäbe, würden wir uns vielleicht mit Morsezeichen verständigen...
Jeder Laut unserer Sprache klingt wie er klingt, weil dabei bestimmte Obertöne erzeugt werden. Diese müssen aber innerhalb eines bestimmten Tonhöhenbereiches liegen, der "Formantregion" heißt. Sopranistinnen singen teilweise so hoch, dass man sie nicht mehr verstehen kann. Das liegt daran, dass die Obertöne, die darüber entscheiden, ob man u, i und ü auseinander halten kann so hoch liegen, dass eine Differenzierung nicht mehr möglich ist.
Obertöne singen
Wenn man einzelne Vokale und die Übergänge zwischen ihnen oder Konsonanten wie n oder ñ
in tiefer Lage singt, kann man Obertöne hören und durch Veränderung der Mundstellung von einem
zum andern wandern. Man braucht dazu Ruhe, eine gute Akustik hilft, und losprusten ist verboten.
Natürlich lassen sich Obertöne wunderbar mit Saiteninstrumenten
produzieren.
Oktavstreifen
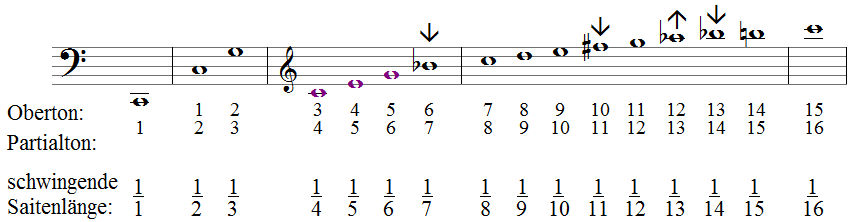
Zwischen den Noten stehen Taktstriche, um die Oktavstreifen von einander abzugrenzen. Im ersten Oktavstreifen findet sich nur der Grundton, im zweiten die Oktave des Grundtons und die Oktavquinte. Im dritten Oktavstreifen stehen vier Töne: lila eingefärbt die Töne des Durdreiklangs, sowie die kleine Septime. Im nächsten Oktavstreifen stehen dann 8 Töne, und im folgenden wären 16 Töne zu finden. Die Anzahl verdoppelt sich mit jeder Oktave, und die Reihe ist nach oben theoretisch bis in den Bereich des Ultraschalls fortsetzbar.
Von der Notation abweichende Töne
Die Töne, über denen ein Pfeil steht, sind deutlich tiefer oder höher als die entsprechenden Töne auf einem gleichschwebend gestimmten Klavier. Der 13. Partialton wird häufig als " a mit ↓" wiedergegeben, er liegt aber tatsächlich näher am as. Schon die große Terz (5. Partialton) ist deutlich tiefer in dieser "reinen" Stimmung als in der temperierten. Die kleine Septime, auch als "Natursepte" bezeichnet, klingt merkwürdig konsonant und in sich ruhend, wesentlich weniger dissonant, als man es sonst von kleinen Septimen gewohnt ist.
In der Zeile "Oberton" beginnt die Zählung nach dem Grundton. In der Zeile "Partialton" darunter zählt der Grundton als 1. Partialton, die Oktave als zweiter usw. Das hat den Vorteil, dass damit gleichzeitig die Schwingungsverhältnisse impliziert sind, die in der untersten Zeile "schwingende Saitenlänge" als Bruch angegeben sind: Beim Grundton schwingt die gesamte Saite (oder Tonsäule bei einem Blasinstrument), bei der Oktavquinte schwingt die Saite in Dritteln.
Das Grundton-C schwingt mit 66 Hertz (die Saite schwingt 66 Mal in der Sekunde). Wenn man die Saite in der Mitte leicht berührt, erzeugt man den 2. Partialton, also die Oktave: die halbe Saite schwingt doppelt so schnell (132 Hz). Der Drittelungspunkt findet sich auf einer Gitarre beim siebten und beim 19. Bund. Wenn man eine Saite hier berührt, schwingt die Saite nur mit Drittellänge, und der 3. Partialton, die Oktavquinte, ist zu hören (Man kann die Saite gerne beim 7. und 19. Bund gleichzeitig berühren und anschlagen - die drei Drittel der Saite schwingen trotzdem!). Dieser erste Ton, der nicht mehr dem Grundton entspricht, ist der viel zitierte "nächste Verwandte", den man für den Quintenzirkel und alles Mögliche bemüht.
Reine und groß/kleine Intervalle
Zwischen 4. und 5. Partialton liegt die große, zwischen 5. und 6. die kleine Terz, ebenso sind große und kleine Sekunden zu finden. Quinten, Quarten und Oktaven gibt es aber nur als "reine" Intervalle. Dass man die Intervalle in zwei Gruppen einteilt, nämlich solche, die nur als "reine Intervalle" auftreten und andererseits die "groß / kleinen" Intervalle, beruht also auch auf den physikalischen Gegebenheiten der Obertonreihe. Und die ist nun mal ein ähnlich grundlegendes Phänomen wie die Farbabfolge im Regenbogen.